1.4.1 Packing Rectangles 铺放矩形块
提交数: 58, 通过率: 37.93%, 平均分: 39.36
题目描述:
给定4个矩形块,找出一个最小的封闭矩形将这4个矩形块放入,但不得相互重叠。所谓最小矩形指该矩形面积最小。
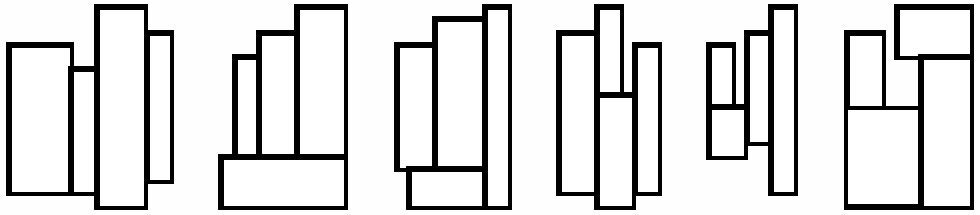
4个矩形块中任一个矩形的边都与封闭矩形的边相平行,图1显示出了铺放4个矩形块的6种方案。这6种方案是唯一可能的基本铺放方案。因为其它方案能由基本方案通过旋转和镜像反射得到。
可能存在满足条件且有着同样面积的各种不同的封闭矩形,你应该输出所有这些封闭矩形的边长。
输入格式:
共有4行。每一行用两个正整数来表示一个给定的矩形块的两个边长。矩形块的每条边的边长范围最小是1,最大是50。
输出格式:
总行数为解的总数加1。第一行是一个整数,代表封闭矩形的最小面积(子任务A)。接下来的每一行都表示一个解,由数P和数Q来表示,并且P≤Q(子任务B)。这些行必须根据P的大小按升序排列,P小的行在前,大的在后。且所有行都应是不同的。
样例输入:
1 2 2 3 3 4 4 5
样例输出:
40 4 10 5 8时间限制: 1000ms
空间限制: 32MB
来源: USAO1- ioi1995