瓷砖

题目描述:

小 A 在当设计师，在研究瓷砖时他发现有的时候不是一定要规规整整地贴瓷砖才好看，斜着贴也可以很好看。这次他面临的任务是 \(n\times m\) 的格点图，可以选用一个任意边长的正方形用任意角度（边不需要水平或者竖直）尝试覆盖，但前提是四个顶点均在格点上。他想找到所有合法的方案，以便之后去分析哪种方案更加美观。

两种方案视为相同当且仅当两种方案占用了相同的四个格点。由于方案数很多，答案对 \(10^9+7\) 取模。

一张 \(3\times 4\) 的格点图示例如下：

输入格式:

输入一行，读入两个数， \(n,m\) ( \(2\leq n,m \leq 10^9+7\)) ，分别代表长和宽包含的格点数。

输出格式:

输出一行，方案数模 \(10^9+7\) 的结果。

数据范围:

- 对于 \(20\%\) 的数据有：\(1\le n,m \le 100\)
- 对于 \(40\%\) 的数据有：\(1\le n,m \le 5000\)
- 对于 \(60\%\) 的数据有：\(1\le n,m \le 2\times 10^6\)
- 对于 \(100\%\) 的数据有：\(1\le n,m\le 10^9 + 7\)

样例输入:

样例1：
4 4

样例2：
3 5

样例输出:

样例1：
20

样例2：
14

提示:

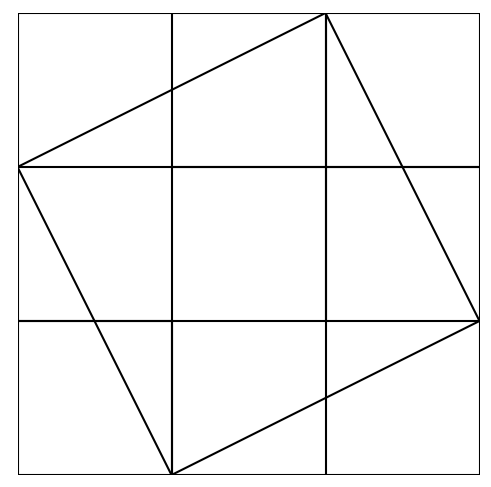
下图为样例一的其中一种合法的方案：

时间限制: 1000ms
空间限制: 512MB

---