鸡爪传说中的宝藏

题目描述:

在一个遥远的国度，有一个神秘的传说，关于一座隐藏在深山老林中的神秘宝藏。传说中，只有那些能够解开鸡爪之谜的勇者才能找到这个宝藏。

据说，宝藏所在的老林中隐藏着许多神奇的鸡爪形状的地形。这些鸡爪形状的地形是一种迷宫，构成了前往宝藏的通道。勇者们必须最大限度地利用鸡爪的形状，才能找到正确的路径，并在通道中避免陷入困境。

为了解开鸡爪之谜，勇者们被赋予了一项任务：使用给定的边，构建一个简单无向图，以最大化图中的鸡爪数。他们需要巧妙地选择边的顶点连接方式，以形成尽可能多的鸡爪形状。

只有当勇者们成功构建出鸡爪数量最多的图形时，他们才能获得通向宝藏的线索。但是，解开鸡爪之谜并不容易，因为他们必须在给定的边限制下，选择正确的连接方式。

现在，你作为一名勇者，接受了这个挑战。你必须聪明地选择边的连接方式，以构建出鸡爪数量最多的图形，找到通向宝藏的线索。

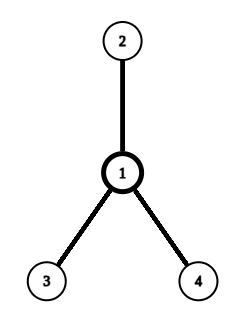
**该图为一个鸡爪的示例,加粗部分被认为在当前鸡爪中**

一个鸡爪是由 \(4\) 个部分组成，一个点与三个与该点相邻的边，三个边的另一端点被认为**不在**鸡爪中。

一个图上的鸡爪数是该图最多成形成几个鸡爪，使得图上每个点与边最多在一个鸡爪中。

现在给你 \(n\) 条边，你可以使用任意个点，构造一个简单无向图（没有自环重边），要求最大化该图的鸡爪数，并输出\(n\)条边的两端点。如果有多解，请让输出的 \(2n\) 个数字在**行优先遍历**的顺序下，**字典序最小**。

这里**行优先遍历**的顺序是指：假如说我们最后输出的答案为

1 2
1 3
1 4

那么我们按行优先遍历的顺序得到的答案序列为 \(\{1,2,1,3,1,4\}\)。

字典序：序列 \(A\) 的字典序小于序列 \(B\)，当且仅当存在 \(i\) (\(1\le i \le n\))，使得 \(A_i \lt B_i\) ，且对任意的 \(j\) (\(1 \le j \lt i\))，\(A_j=B_j\) 。

准备好了吗？穿越老林的鸡爪之谜正等待着你的解密。带上你的勇气和智慧，踏上这段充满挑战的旅程吧！

输入格式:

第一行为一个整数 \(T(1 \le T \le 2 \times 10^5)\) ，表示测试样例个数。

每个样例一行，为一个整数 \(n\)(\(1 \le n \le 2 \times 10^5\))。保证所有样例的\(n\)的和\(\le 2 \times 10^5\)。

输出格式:

每个样例输出 \(n\) 行，每行两个正整数，表示该无向边连接的两个顶点（顶点从 \(1\) 开始编号）

数据范围:

- 对于 \(20\%\) 的数据有：\(1\le n\le 10,\sum n\le 100\)。
- 对于 \(40\%\) 的数据有：\(1\le n\le 500,\sum n\le 5000\)。
- 对于 \(60\%\) 的数据有：\(1\le n\le 5000,\sum n\le 50000\)。
- 对于 \(100\%\) 的数据有：\(1\le n\le 2\times 10^5,\sum n\le 2\times 10^5\)。

样例输入:

2
3
5

样例输出:

1 2
1 3
1 4
1 2
1 3
1 4
1 5
1 6

时间限制: 1000ms
空间限制: 512MB

---