迷失的国王

题目描述:

在一个古老的王国里，有一位慈祥的国王。某天，国王突然迷失在了自己的宫殿中。宫殿是一个 \( n \times m\) 的棋盘，国王想要找到两个相同的宝藏，这样他才能找到回家的路。

国王知道两个相同的宝藏在宫殿上的位置，并且他们之间的曼哈顿距离为 \(k\)。国王希望知道有多少种放置两个宝藏的方式，使得它们的曼哈顿距离恰好为 \(k\)。

国王请求你作为王国最聪明的智者，设计一个算法来解决这个问题。

其中在平面上，坐标 \((x_1, y_1)\) 的点 \(P_1\) 与坐标 \((x_2,y_2)\) 的点 \( P_2\) 的曼哈顿距离为：

其中 \(|x|\) 表示绝对值符号，当 \(x<0\) 时，\(|x|=-x\)，否则 \(|x|=x\)。

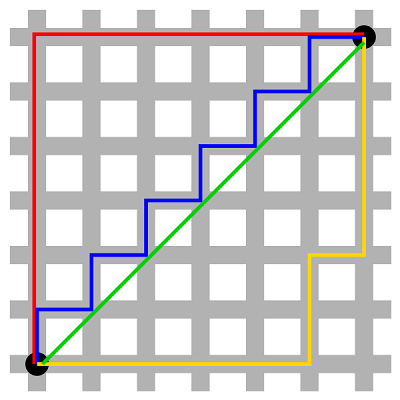
图中左下角的点 \(P_1\) 坐标为 \((0,0)\) ，右上角 \(P_2\) 坐标为 \((6,6)\)，那么这两点之间的曼哈顿距离为 12。

图中红、蓝与黄线的长度与 \(P_1\) 和 \(P_2\) 的曼哈顿距离相等。

输入格式:

三个正整数 \(n,m,k\) (\(1\le n,m,k\le10^6\))

输出格式:

一个整数表示方案数。

数据范围:

• 对于 \(20\%\) 的数据有：\(1\le n,m,k\le 100\)。

• 对于 \(40\%\) 的数据有：\(1\le n,m,k\le 500\)。

• 对于 \(60\%\) 的数据有：\(1\le n,m,k\le 5000\)。

• 对于 \(100\%\) 的数据有 \(1\le n,m,k\le 10^6\)。

样例输入:

样例1：
8 8 14

样例2：
8 8 3 

样例3：
4 3 3

样例输出:

样例1：
2

样例2：
248

样例3：
17

提示:

样例一有两种方案，或者放在左上角和右下角，或者放在左下角和右上角。