摆放L II

题目描述:

题目背景

因为zhr大佬出了一道分治的“摆放L”，于是，ljc想出一道dp题……

有一个n×m的棋盘，上面有k个障碍物，其他地方要铺放如下图所示的四种L字形的骨牌：

 

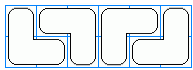
判断有多少种方法让它正好铺满，如下图为6×6的棋盘的一种铺法：

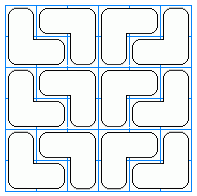
输入格式:

第一行为一个数T，表示一共有T组数据。

每组数据第一行为三个数n、m和k，用空格隔开。

后k行有两个数，表示每个障碍物所在的行和列，用空格隔开。保证不会有两个障碍物在同一个格子上。

输出格式:

一共T行，分别表示每组数据的答案。

样例输入:

4
9 2 0
7 2 2
6 1
5 1
2 6 0
4 4 1
2 4

样例输出:

8
2
4
1

提示:

对于20%的数据，n×m<=20，T<=15。

对于另外20%的数据，n和m中有一个为2或3，k=0，T<=15。

对于所有数据，6<=n×m<=100，n×m除以3的余数为k，T<=50。

时间限制: 1000ms
空间限制: 256MB

---

来源: by ljc