八皇后问题

提交数: 1353, 通过率: 53.44%, 平均分: 54.53

题目描述:

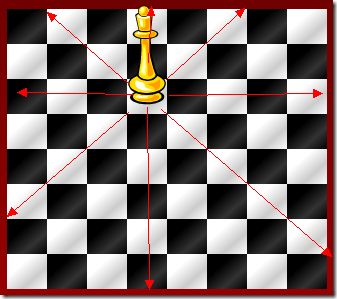
要在国际象棋棋盘中放八个皇后，使任意两个皇后都不能互相吃，皇后能吃同一行、同一列，同一对角线上（两个方向的对角线）的任意棋子。现在给一个整数n(n<=92)，输出前n种的摆法。

1497315157753049269.jpeg

输入格式:

输入一个整数n。

输出格式:

输出共n行。

每行8个数，表示每行所放的列号，每个数输出占4列。

样例输入:

3

样例输出:

   1   5   8   6   3   7   2   4
   1   6   8   3   7   4   2   5
   1   7   4   6   8   2   5   3

提示:

1497344390503583632.png

八皇后总共的摆放方案有92种。

 

请仔细阅读下面程序：

时间限制: 1000ms
空间限制: 128MB

来源: 原创