最少转车次数

题目描述:

小华从某起点到某目的地需要经过若干次公交转车( 乘车不存在绕圈现象，但不保证可以到达目的地 ），显然坐车的方案可能不唯一。如下图所示，从起点A到目的地H可以选择公交线路“A -> D -> E -> F -> H”，也可以选择公交线路“A -> D -> G -> H”。前者需要在“D”、“E”、 “F”三个公交车站下车后转车3次，而后者只需要在“D”和“G”两个公交车站下车后转车2次，且是所有乘坐公交车方案里转车次数最少的一种方案。

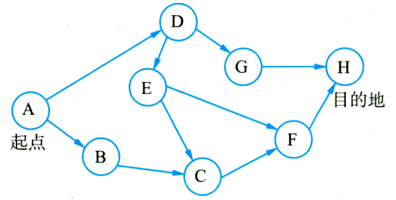
现给出某公交车坐车方案图，求从起点A到目的地的最少转车方案。

输入格式:

第一行三个整数 n, m，n表示图中的顶点数，m表示有向图的边数；

接下来共m行,每行两个整数(i,j)，为图G中的一条有向边；

最后一行一个字母，表示目的地。

输出格式:

一个数，表示最少的转车次数。

数据范围:

图中顶点数小于26个，边数小于50条。

样例输入:

8 10
A B
A D
B C
C F
D E
E C
E F
D G
F H
G H
H

样例输出:

2

提示:

请完善以下程序：

#include <bits/stdc++.h>
using namespace std;
int a[27][27],b[27], n, m, to, c;
int q[27], head, tail;
bool f[27];
char x, y ;

int main() {
	cin >> n >> m;
	for ( int i=1; i<=m; i++) {       //读入m条边，建图
		cin >> x >> y;  //读入两个能够直达的车站编号
		________(1)__________ 
	}
	head =0;
	tail = 0;
	q[tail] = 0 ;
	______(2)_______
	f[0] = true;
	b[0] = 0;
	cin >> x;  //读入目标车站编号
	to = x - 'A';
	while ( head < tail  ) {   //广搜：队列不为空，并且没有找到目标车站
		c = q[ head ];
		______(3)_______
		if ( c == to ){  //找到终点
			cout << b[c] - 1;
			return 0;
		}
		for ( int j=0; j<n; j++) {    //队头的元素，和其他所有的顶点看看有没有边，有则把它拉进队列
			if ( ______(4)_______ ) {
				q[ tail ] = j;
				tail += 1;
				f[j] = true;
				b[j] = b[c] +1;
			} 
		}
	}
	printf( "NO PATH!" );
	return 0;
}

时间限制: 1000ms
空间限制: 256MB

---

来源: 高中教材