求凸性函数的最值（三分）

题目描述:

如题，给出一个 N 次函数，保证在范围[l,r] 内存在一点 x，使得 [l, x] 上单调增，[x, r] 上单调减。试求出 x 的值。

输入格式:

第一行一次包含一个正整数 N 和两个实数 l, r含义如题目描述所示。

第二行包含 N + 1 个实数，从高到低依次表示该 N 次函数各项的系数。

输出格式:

输出为一行，包含一个实数，即为 x 的值。四舍五入保留 5 位小数。

样例输入:

3 -0.9981 0.5
1 -3 -3 1

样例输出:

-0.41421

提示:

对于 100% 的数据，7≤N≤13。

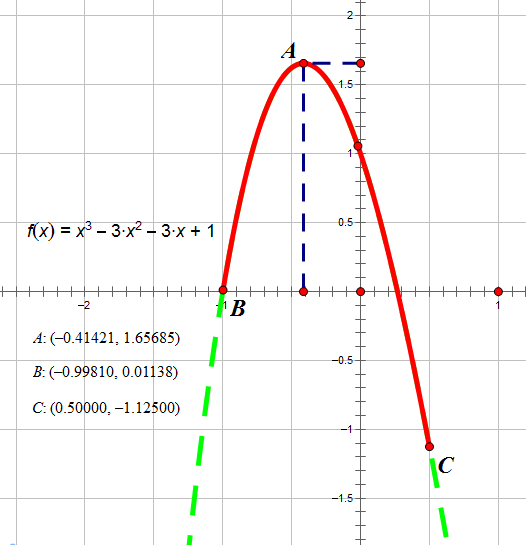
如图所示，红色段即为该函数 f(x) = x^3 - 3 x^2 - 3x + 1 在区间 [−0.9981,0.5] 上的图像。

当 x=−0.41421 时图像位于最高点，故此时函数在 [l,x] 上单调增，[x,r] 上单调减，故 x=−0.41421，输出−0.41421。

时间限制: 1000ms
空间限制: 256MB

---

来源: 洛谷