平板涂色

题目描述:

给定一个矩形块，它里面包含了n个小矩形块，现在要求将每个小矩形块涂上给定的颜色。

涂色过程中，小矩形必须是整块整块的涂，并且为了避免颜料渗漏导致颜色混合，一个矩形只有当它上面的所有矩形都被涂色之后它才能被涂色。每只刷子只能涂一种颜色，问至少需要换多少次刷子。（第一次拿起刷子也算一次）。

注意：如果一把刷子被拿起超过一次，则每一次都必须记入总数。

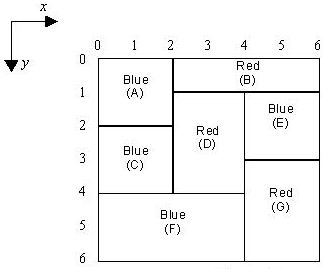
输入格式:

第一行为矩形的个数N。

下面有N行数据描述N个矩形。每个矩形用5个整数描述：左上角的y坐标和x坐标，右下角的y坐标和x坐标，以及预定颜色。

颜色号为1到20的整数。平板的左上角坐标总是（0，0），坐标的范围是0...99，N小于16。

输出格式:

一个整数，表示拿起刷子的最少次数。

样例输入:

7
0 0 2 2 1
0 2 1 6 2
2 0 4 2 1
1 2 4 4 2
1 4 3 6 1
4 0 6 4 1
3 4 6 6 2

样例输出:

3

时间限制: 1000ms
空间限制: 256MB

---