递归n阶勒让德多项式

题目描述:

用递归方法求n阶勒让德多项式的值，递归公式如下：

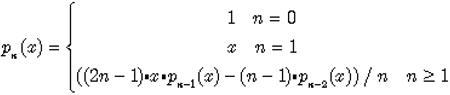
当n=0的时候，p(0,x)=1

当n=1的时候，p(1,x)=x

当n>1的时候，p(n,x)=((2*n-1)*x*p(n-1,x)-(n-1)*p(n-2,x))/n

输入格式:

在一行内有一个正整数n和一个实数x，用空格分隔。保证n不超过10。

输出格式:

输出p_n(x)的值，小数点后保留4位小数。

请注意行尾输出换行。

样例输入:

5 2.5

样例输出:

637.0117

时间限制: 1000ms
空间限制: 32MB

---

来源: 原创